We hear probabilities in forecasts all the time: “There’s a 10% chance of rain”, “your favorite team has a 40% chance of winning tonight”, etc. But what does that actually mean? Are these numbers just plucked out of the sky? And if there was only a 10% chance of rain, then was the weatherman wrong when my picnic got soaked?
Typically, they’re calculated by simulating the data. We’ll use Fangraph’s playoff odds as an example here. They first take a look at a team’s roster and each player’s individual projections to work out how good the team is expected to be. Since this number is their expected true talent and teams can under-perform or over-perform, they then simulate the season 20,000 times. From there, they can count how often a team wins their division, divide by 20,000, and now you have the odds of winning.
This is all well and good, but we’ll only have one 2022 MLB season, multiverse theories aside. We can’t actually play the same season more than once, let alone 20K times. But we can say that given one season, we expect certain outcomes.
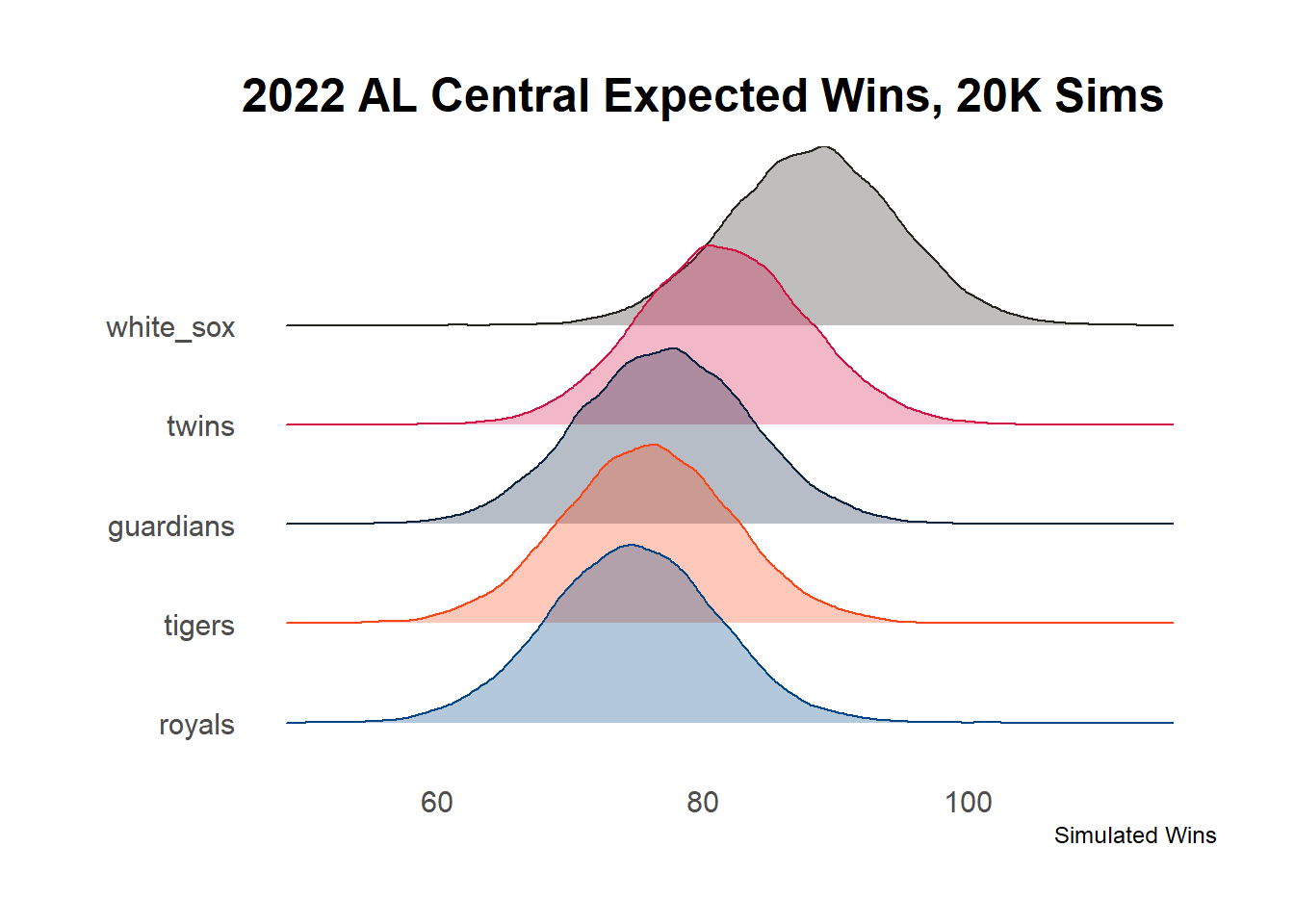
For instance, the Tigers win the AL Central in 3.6% of simulations. This doesn’t mean they’re bound to lose, but it also means that I shouldn’t plan my October around watching them in the playoffs. And if they do make the postseason, it doesn’t mean the projections were wrong - after all, they won in about 4 out of 100 simulations.
In this case, seeing the expected number of wins for each team provides some helpful context. We see the White Sox are heavy favorites, though the Twins stand a fighting chance. Since there are five teams total and the Tigers have to outperform them all, we can see the odds are not exactly in their favor - unless, of course, they’re actually quite a bit better than the projections expect.
If we shift to weather, this means the weatherman isn’t wrong when he calls for a 10% chance of rain. We may have only had one instance of that day, and unfortunately we got dumped on, but there was always a 1 in 10 chance this would happen. (As well as a 9 in 10 chance it wouldn’t rain - when we say one thing is x percent likely to happen, we’re also saying it’s y percent likely to not happen).
One important caveat in forecasting is that it assumes the underlying process remains more or less the same. If its assumptions are violated - such as changing the rules in baseball to give batters four strikes instead of three - then future forecasts won’t be much help since they reflect a different world.
Of course, just because we can’t necessarily say how right a forecaster is based off of one forecast doesn’t mean we can’t measure their performace. For cases like projecting a baseball season or weather forecasts, we can always check past forecasts against actual results to see just how good the system is. FanGraphs has offered this analysis in the past, and you can find weather forecast accuracy results as well. So if your weatherman calls for rain 90% of the time and it only rains 5%, perhaps it’s time to find a new forecaster.
This macro-view also helps protects us against recency bias. If we just got rained out when the forecast called for a 20% chance of rain, we may conclude our weatherman is always wrong - while ignoring the other 100 correct forecasts he’s had this year. Or we may pick the one thing they got right and ignore the 100 they got wrong. Nobody can predict the future perfectly, but with a little bit of structure we can see who can make the best projections.