Show the code
set.seed(202209)
sample(c('A', 'B', 'C'), 12, replace = TRUE, prob = c(0.5, 0.3, 0.2)) [1] "A" "C" "B" "A" "C" "B" "A" "B" "A" "A" "C" "B"Mike Trout will go down in the history books as one of the top players in the game. He currently ranks 35th on Fangraph’s career WAR leaderboard, and he’s still got more years in the tank. Our interest today, though, is not in his historical greatness, but in how well we can predict his future greatness.
You almost feel sorry for whoever’s pitching to him here.
There are multiple ways to sim a season, but we’re going to keep this very simple. Firstly, we’re going to limit our data to his last three seasons, since they’ll most likely be indicative of his future performance. We’re going to use 2019-2021 and simulate 2022, while that season is inconveniently still in progress, we can also use the actual numbers to see how well we’ve done.
Since a plate appearance can have multiple outcomes - single, double, triple, home run, strikeout, walk, etc. - we’ll need to set our sim to return the outcome for each go around. The “sample” function in R lets us provide a set of strings and their probability of occurring. If we say that there’s a 50% chance of ‘A’, 30% chance of ‘B’, and 20% chance of ‘C’, and we want to draw 12 letters from our imaginary urn* of letters, we get:
*Outside of crematoriums, probability books have the most references to urns.
7 As, 4 Bs, and 1 Cs - pretty close to what we’d expect. If we had a larger sample we’d be closer still, though not exactly - there’s still random variation in play. So all we need to do now is get Trout’s stats (via the ever useful Lahman package) and the odds of a plate appearance ending in a single, double, and so on. Since Trout’s had 445 PA this year, we’ll run this sim 445 times, collect the results, then do it another 9,999 times. Knowing his current PA is cheating, and if we were being more formal we’d randomize the number of PA for each simulated season.
*That’s almost 4.5 million plate appearances. That would take Trout over 13 years if he went non-stop and used ghost runners when he got a hit, and I think he’d be annoyed at us doing all this just to estimate his performance. The sim takes under 5 minutes on my laptop, which is a considerable time saving.
Show the code
library(baseballr)
library(gt)
library(hrbrthemes)
library(Lahman)
library(tidyverse)
#we'll need woba values later
woba_weights <- fg_guts() %>%
as_tibble() %>%
select(-runSB, -runCS, -lg_r_pa, -lg_r_w, -cFIP)
#get Trout's current season stats for reference later
trout_2022 <- fg_batter_leaders(x = 2022, y = 2022, qual = 400) %>%
filter(Name == 'Mike Trout')
#get stats from the Lahman database and prep
trout_stats <- Lahman::Batting %>%
filter(playerID == 'troutmi01') %>%
filter(yearID >= 2019) %>%
inner_join(woba_weights, by = c("yearID" = "season")) %>%
mutate(X1B = H - X2B - X3B - HR,
PA = AB + BB + HBP + SH + SF,
UBB = BB - IBB,
TB = H + X2B + 2 * X3B + 3 * HR) %>%
mutate(woba_pa = ((X1B * w1B)+ (X2B * w2B) + (X3B * w3B) + (HR * wHR) +
((BB - IBB) * wBB) + (HBP * wHBP))) %>%
select(-yearID, -stint, -teamID, -lgID, -GIDP, -wBB, -wHBP, -w1B, -w2B, -w3B, -wHR,
-woba_scale, -lg_woba) %>%
group_by(playerID) %>%
summarise(across(everything(), sum)) %>%
mutate(AVG = ifelse(AB > 0, round(H/AB, 3), NA),
SLG = ifelse(AB > 0, round(TB/AB, 3), NA),
OBP = ifelse(PA > 0, round((H + BB + HBP)/(PA - SH), 3), NA),
OPS = round(OBP + SLG, 3),
BABIP = ifelse(AB > 0, round((H - HR)/(AB - SO - HR + SF), 3), NA),
WOBA = round(woba_pa / (AB + BB - IBB + SF + HBP), 3)
) %>%
select(-woba_pa)
#set columns to use in odds and simmed stats
player_colnames <- c('X2B', 'X3B', 'HR', 'UBB', 'SO', 'IBB', 'HBP', 'SH', 'SF', 'X1B', 'outs_in_play')
trout_odds <- trout_stats %>%
ungroup()%>%
mutate(outs_in_play = PA - X1B - X2B - X3B - HR - BB - SO - IBB - HBP - SH - SF) %>%
select(player_colnames, PA) %>%
mutate(across(everything(), ~ . / PA)) %>%
select(-PA)
sim_seasons <- function(player_odds, sims = 10000, pa = 600){
simmed_seasons <- data.frame(matrix(ncol = length(player_colnames),
nrow = 0,
dimnames = list(NULL, player_colnames))) %>%
as_tibble()
for(i in 1:sims){
tmp_sim <- sample(colnames(player_odds),
pa,
replace = TRUE,
prob = as.double(player_odds)) %>%
as_tibble() %>%
group_by(value) %>%
summarise(n = n()) %>%
pivot_wider(names_from = value, values_from = n) %>%
mutate(sim_id = i) %>%
replace(is.na(.), 0)
simmed_seasons <- bind_rows(simmed_seasons, tmp_sim)
}
simmed_seasons
}
simmed_data_counting <- sim_seasons(trout_odds, pa = 445)
simmed_data_agg <- simmed_data_counting %>%
replace(is.na(.), 0) %>%
mutate(PA = 445,
BB = IBB + UBB,
AB = PA - BB - HBP - SF) %>%
mutate(H = X1B + X2B + X3B + HR,
TB = H + X2B + 2 * X3B + 3 * HR,
SH = 0) %>%
mutate(AVG = ifelse(AB > 0, round(H/AB, 3), NA),
SLG = ifelse(AB > 0, round(TB/AB, 3), NA),
OBP = ifelse(PA > 0, round((H + BB + HBP)/(PA - SH), 3), NA),
OPS = round(OBP + SLG, 3),
BABIP = ifelse(AB > 0, round((H - HR)/(AB - SO - HR + SF), 3), NA),
WOBA = round(((X1B * 0.888)+ (X2B * 1.271) + (X3B * 1.616) + (HR * 2.101) +
((BB - IBB) * 0.690) + (HBP * 0.722)) / (AB + BB - IBB + SF + HBP), 3)
) %>%
select(-outs_in_play)
trout_2022_long <- trout_2022 %>%
select(Name, `1B`, `2B`, `3B`, AVG, BABIP, BB, H, HBP, HR, IBB, OBP, OPS, SF, SH, SLG, SO, wOBA) %>%
pivot_longer(!Name, names_to = 'metric', values_to = 'actual') %>%
select(-Name)
simmed_data_agg %>%
select(-AB, -PA, -TB, -UBB, -SH) %>%
pivot_longer(!sim_id, names_to = 'metric', values_to = 'value') %>%
group_by(metric) %>%
mutate(metric = case_when(metric == 'X1B' ~ '1B',
metric == 'X2B' ~ '2B',
metric == 'X3B' ~ '3B',
metric == 'WOBA' ~ 'wOBA',
TRUE ~ metric)) %>%
summarise(median_outcome = median(value),
lower_05 = quantile(value, 0.05),
upper_95 = quantile(value, 0.95)) %>%
left_join(trout_2022_long) %>%
gt() %>%
tab_style(
locations = cells_column_labels(columns = everything()),
style = list(
cell_text(weight = "bold")
)
) %>%
fmt_number(
columns = 2:5,
rows = c(4,5,11,12,14,16),
decimals = 3,
use_seps = FALSE
) %>%
fmt_number(
columns = 2:5,
rows = c(1,2,3,6,7,8,9,10,13,15),
decimals = 0,
use_seps = FALSE
)| metric | median_outcome | lower_05 | upper_95 | actual |
|---|---|---|---|---|
| 1B | 52 | 41 | 64 | 49 |
| 2B | 20 | 13 | 28 | 21 |
| 3B | 2 | 0 | 5 | 2 |
| AVG | 0.304 | 0.265 | 0.344 | 0.273 |
| BABIP | 0.335 | 0.283 | 0.387 | 0.310 |
| BB | 79 | 66 | 93 | 48 |
| H | 107 | 93 | 122 | 108 |
| HBP | 10 | 5 | 15 | 6 |
| HR | 32 | 24 | 42 | 36 |
| IBB | 10 | 6 | 16 | 6 |
| OBP | 0.440 | 0.402 | 0.479 | 0.360 |
| OPS | 1.088 | 0.959 | 1.226 | 0.969 |
| SF | 4 | 1 | 7 | 0 |
| SLG | 0.648 | 0.546 | 0.758 | 0.609 |
| SO | 100 | 86 | 115 | 128 |
| wOBA | 0.455 | 0.408 | 0.506 | 0.407 |
This worked pretty well. The sim had a median projection of 51 singles, with 90 percent of sims coming between 40 and 62. He’s actually hit 49, so we’re not too far off. The notable exception is walks - we expected 65 to 91, but he’s only drawn 47, which means his OBP of .360 is outside our expected range of .393 and .470.
Note that a .360 OBP, while pedestrian by Trout’s standards, is still good for 16th in MLB this year for all hitters with at least 400 PA, so he’s not exactly slouching. While that’s not entirely out of our forecast, that’s just barely true, with only 0.01% coming below the actual.
Show the code
simmed_data_agg %>%
ggplot(aes(x = OBP))+
geom_density(fill = '#BA0021', alpha = 0.6)+
geom_vline(xintercept = trout_2022$OBP)+
theme_ipsum()+
ggtitle('Trout Expected OBP')+
ylab('')
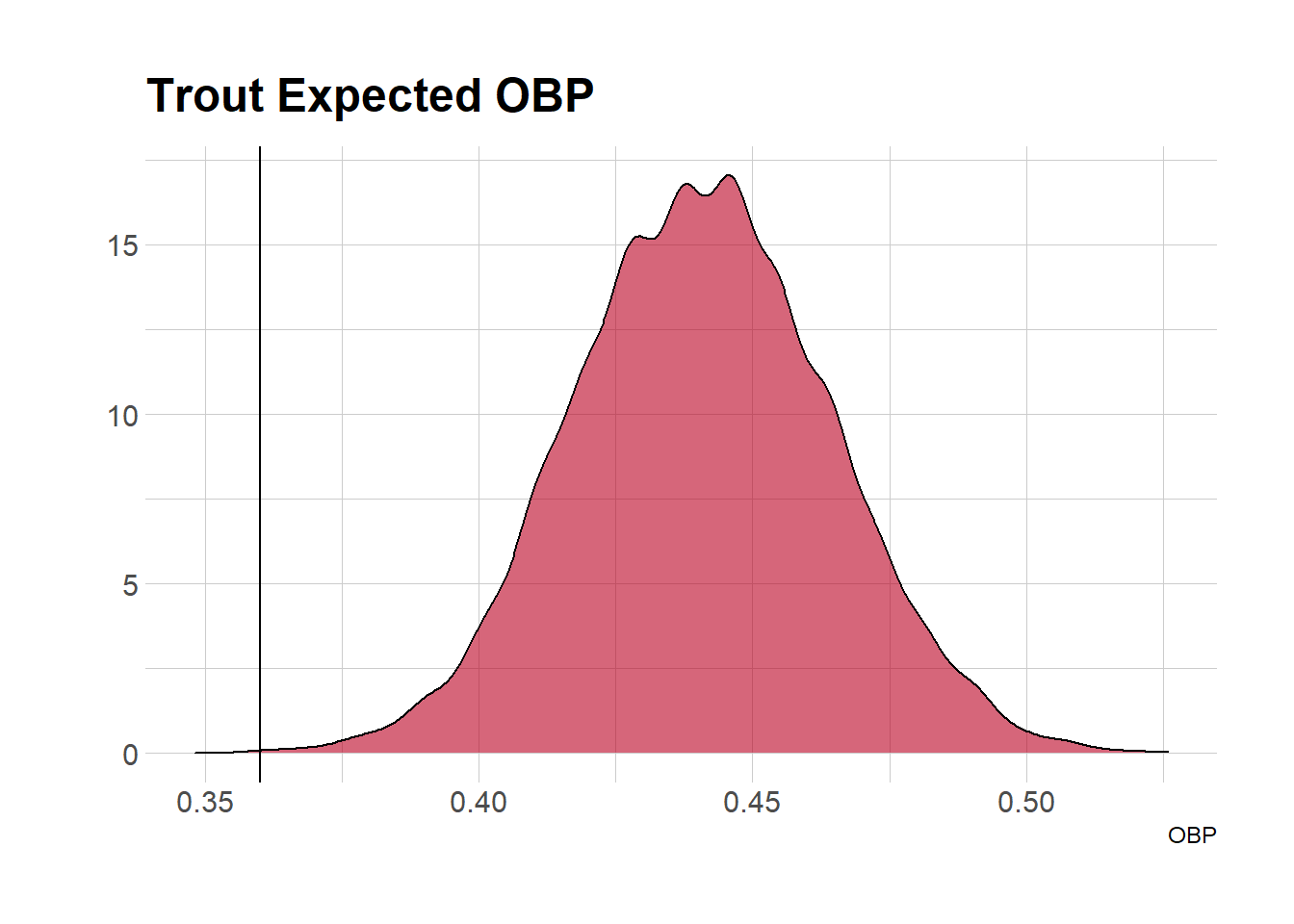
This shows us several important things about forecasting. Firstly, note that we assumed he’d keep doing what he’s been doing. This is true in a lot of areas, but not everything. The model certainly didn’t see the drop in walks coming. Humans - and systems - can and do change, and without manual intervention in our model or additional inputs, we can’t account for him becoming a more aggressive swinger.
Secondly, having a range is important to be realistic. A range of 23 to 41 home runs is pretty large, but 445 PAs is still a pretty small sample. The way Trout hits isn’t random as such, so it’s not exactly akin to drawing a random number and seeing what it is, but the distribution of outcomes can still change in subtle ways that impact the overall line.
If we were developing this further, we’d account for other elements such as aging, batted ball velocity and launch angle, etc. The first pass will often give you pretty good insights, but if it’s off somewhere, the question is not “why doesn’t reality match my model”, but “why doesn’t my model match reality”.